y=sinx+cosxの合成、グラフ、最大値など

合成

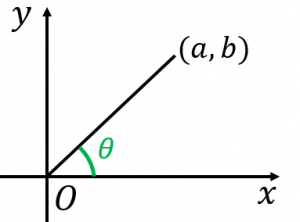
三角関数の合成公式：
$a\sin x+b\cos x$$=\sqrt{a^2+b^2}\sin(x+\theta)$
で、$a=b=1$ とすると、
$\sin x+\cos x$$=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)$
という式を得ることができます。

$y=\sin x+\cos x$ という関数について考えるときは、この変形が基本になります。

グラフ

$y=\sin x+\cos x$ という関数のグラフの概形を書いてみます。

先程の変形より、$y=\sin\left(x+\dfrac{\pi}{4}\right)$ という関数のグラフを書けばOKです。
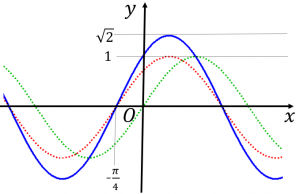
これは、$y=\sin x$ のグラフ（緑の点線）を $x$ 軸方向に $-\dfrac{\pi}{4}$ 平行移動（赤の点線）して、$y$ 軸方向に $\sqrt{2}$ 倍に拡大したものなので、図の青い実線のようになります。

最大値、最小値

次は、$y=\sin x+\cos x$ という関数のとりうる値の範囲について考えてみます。

この場合も、$y=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)$ という変形をしてから考えることで、最大値は $\sqrt{2}$、最小値は $-\sqrt{2}$ となることが分かります。

ちなみに、最大値を取るのは $x=\dfrac{\pi}{4}+2n\pi$（$n$ は整数）
最小値を取るのは $x=\dfrac{3\pi}{4}+2n\pi$（$n$ は整数）
です。
※定義域が制限されている場合は値域も狭くなることがあります。

おまけ

コサインによる合成：
$\sin x+\cos x$$=\sqrt{2}\cos\left(x-\dfrac{\pi}{4}\right)$
これは、加法定理を使って右辺を展開すると左辺と一致することが確認できます。

微分：
$(\sin x+\cos x)’=\cos x-\sin x$
それぞれ微分するだけです。

不定積分：
$\displaystyle\int(\sin x+\cos x)dx$$=-\cos x+\sin x+C$
それぞれ積分するだけです。

次回は xsinxの微分、グラフ、積分など を解説します。