2進数において、
$0$ と $1$ を反転させたものを1の補数と言う。
それに $1$ を足したものを2の補数と言う。
1の補数の意味と具体例
2の補数を理解するために、まずは1の補数です。2進法の世界で、$0$ と $1$ を反転させたものを1の補数と言います。
例えば、
$1011$ の1の補数は
$0100$ です。
$10100100$ の1の補数は
$01011011$ です。ただ反転させるだけなので簡単です。
2の補数の意味と具体例
$0$ と $1$ を反転させて $1$ を加えたものを2の補数と言います。
例えば、$1011$ の2の補数は、反転させたもの $0100$ に1を加えたものなので、$0101$ です。
また、$10100100$ の2の補数は、反転させたもの $01011011$ に1を加えたものなので、$01011100$ です。
余談ですが、2の補数は、以下のように定義することもできます:
($k$ 桁で考えているとき)$a$ の2の補数は $2^k-a$
この説明から、$a$ の「2の補数」の「2の補数」は $a$ であることが分かります。
ただ、「$0$ と $1$ を反転させて $1$ を加えたもの」という説明のほうが分かりやすいと思います。
負数の表し方
コンピュータの世界で広く用いられている、8ビットで整数を表す方法を解説します。$-128$ から $127$ までの整数を表すことができます。
正の数は普通に2進数で表します。例えば $3$ は $00000011$ と表します。
負の数については、$-a$ は $a$ の「2の補数」で表現します。
例題1(人間→コンピュータ の変換)
$-6$ を上記の方法で8ビットで表現せよ。
解答
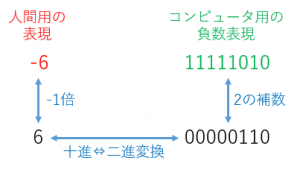
$-6$ は $6$ の「2の補数」で表します。$6$ は $2^2+2$ なので、二進法では $00000110$ です。これの「2の補数」を取ればよいので、
ビット反転:$11111001$
さらに1を加える:$11111010$
が答えになります。
例題2(コンピュータ→人間 の変換)
$11111010$ は10進法でどのような数字を表すか?
解答
左端のビットが1の場合、マイナスの数を表すことになっています。コンピュータ用の負数を普通の2進数に直すのも2の補数を使えばOKです。
ビット反転:$00000101$
1を加える:$00000110$
これを10進法に直すと $2^2+2=6$ となります。よって、答えは $-6$ です。
次回は 二進数のかけ算の2通りのやり方と計算ツール を解説します。
