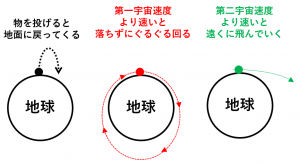
第一宇宙速度とは、地表すれすれを落ちずに軌道上へ乗せるための最小速度のことです。
第二宇宙速度とは、地球の重力圏から完全に脱出するために必要な最小速度を指します。
第一宇宙速度・第二宇宙速度は宇宙開発の基礎概念として非常に重要です。本記事では、両者の意味・数値の理由・計算式の導出まで体系的に解説します。
第一宇宙速度とは
地球の表面から物体を水平方向へ投げると、通常は重力によって落下します。しかし、速度が十分に大きい場合、落ちるよりも速く地球が丸く“地面が遠ざかる”ため、物体は落下せず軌道を周回します。
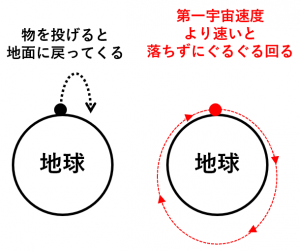
その境界となる速度が
秒速 7.9 km(時速 28,400 km) です。
これより遅いと必ず落下し、これ以上であれば人工衛星と同じように地球を周回することができます。
※宇宙速度の議論では空気抵抗を無視します。このページも同じ前提で説明しています。
第二宇宙速度とは
第一宇宙速度を超えても、速度が足りなければ地球の周囲を楕円軌道で回り続けます。
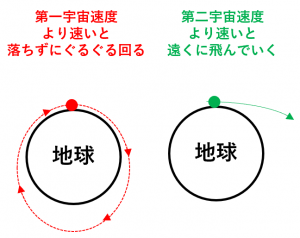
しかし、さらに速くすれば地球の重力エネルギーを上回り、そのまま宇宙へ飛び去ることができます。これに必要な速度が
秒速 11.2 km(時速 40,300 km) です。
これが第二宇宙速度であり、地球脱出速度とも呼ばれます。
第一宇宙速度の計算式
$v_1=\sqrt{\dfrac{GM}{R}}$
で求められます。
ここで、$G$ は万有引力定数、$M$ は地球の質量、$R$ は地球の半径です。
第一宇宙速度の導出:
質量 $m$ の物体が地球表面近くで円運動するとき、必要な向心力は
\[ m\dfrac{v_1^2}{R} \]
です。
一方、地球がその物体を引く重力は
\[ \dfrac{GMm}{R^2} \]
です。
軌道に乗るには、これらが釣り合う必要があるため
$m\dfrac{v_1^2}{R}=\dfrac{GMm}{R^2}$
が成立します。
これを $v_1$ について解くと
\[ v_1=\sqrt{\dfrac{GM}{R}} \]
となり、数値を代入すると約 $7.9\:\mathrm{km/s}$ を得ます。
第二宇宙速度の計算式
$v_2=\sqrt{\dfrac{2GM}{R}}$
で求められます。
第一宇宙速度のちょうど $\sqrt{2}$ 倍になるという美しい関係が成立します。
第二宇宙速度の導出:
質量 $m$ の物体を初速 $v$ で投げ出すとき、運動エネルギーは
\[ \dfrac{1}{2}mv^2 \]
であり、地球表面での位置エネルギーは
\[ -\dfrac{GMm}{R} \]
です。
重力を振り切るには、無限遠で全エネルギーが 0 以上であればよいので、第二宇宙速度 $v_2$ は
$\dfrac{1}{2}mv_2^2=\dfrac{GMm}{R}$
を満たします。
よって
\[ v_2=\sqrt{\dfrac{2GM}{R}} \]
となり、数値計算すると約 $11.2\:\mathrm{km/s}$ です。
なお、これらの式は地球以外の天体(月・火星など)でもそのまま適用できます。天体ごとに重力や半径が異なるため、宇宙速度も変化します。
次回は 運動量と力積の意味を図でわかりやすく解説 を紹介します。
