運動量とは「質量×速度」のことです。運動量は「その物体を止めるのがどれくらい大変か」を表す量と言えます。
このページでは、運動における基本的な物理量である運動量の意味を解説します。また、運動量に関係した重要な量である力積についても解説します。
運動量とは
つまり、質量 $m$ の物体が速度 $v$ で運動しているときの運動量は $mv$ です。
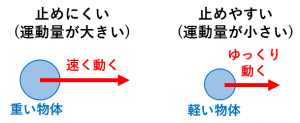
運動量は「その物体を止めるのがどれくらい大変か」を表す量と考えることができます。

同じ速さでも、質量が大きい物体ほど止めるのが大変なので、運動量は大きいです。
同じ質量でも、速さが速いほど止めるのが大変なので運動量は大きいです。
例えば、$2\:\mathrm{kg}$ の物体が、速さ $3\:\mathrm{m/s}$ で運動しているときの運動量は、
$2\times 3=6\:\mathrm{kg\cdot m/s}$
となります。このように、運動量の単位は、$\mathrm{kg\cdot m/s}$ または $\mathrm{N\cdot s}$ が使われます。
力積とは
例えば、$10\:\mathrm{N}$ の力を $2$ 秒間加え続けたときの力積は、
$10\times 2=20\:\mathrm{N\cdot s}$
のように計算できます。
このように、力積の単位は、$\mathrm{N\cdot s}$ になります。
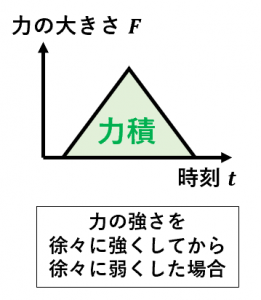
実は、もう少し厳密に言うと、力積は、横軸を時刻、縦軸を力の大きさをとするグラフにおける、横軸とグラフで囲まれた面積となります。
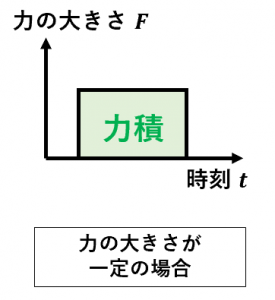
力の大きさが一定の場合には、力積は長方形の面積と等しいので、
力積=力×時間
が成立します。
力積=$\displaystyle\int Fdt$
となります。
$F$ は物体に加えた力です。時刻 $t$ で積分します。
運動量と力積の関係
運動量の変化量=物体に与えた力積の大きさ
という関係が成立します。
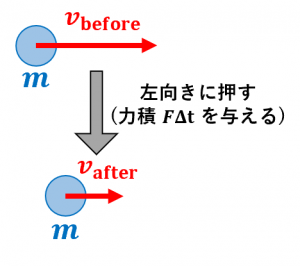
式で書くと、
$mv_{\mathrm{after}}-mv_{\mathrm{before}}=F\Delta t$
という関係が成立します。
力 $F$ が大きいほど、そして力を加えた時間 $t$ が長いほど、運動量が大きく変化します。つまり、力積とは「運動量をどれくらい変えることができるか」を表す量と言えます。
※この法則は、運動方程式を時刻 $t$ で積分することで導出できます。
運動量と力積はベクトル
運動量はベクトル:
速度 $\overrightarrow{v}$ はベクトルなので、運動量 $m\overrightarrow{v}$ もベクトルになります。
力積もベクトル:
力 $\overrightarrow{F}$ はベクトルなので、力積 $\displaystyle\int \overrightarrow{F}dt$ もベクトルになります。
運動量と力積の等式もベクトルの等式:
$m\overrightarrow{v}_{\mathrm{after}}-m\overrightarrow{v}_{\mathrm{before}}=\overrightarrow{F}t$
次回は 遠心力の意味と計算する3つの公式【証明つき】 を解説します。
