熱膨張率（線膨張率、体積膨張率）の意味と伸びた長さの計算

鉄などの物質の温度を上げると、膨張します。このとき、どれくらい膨張するか（長くなるか、大きくなるか）を表すのが、熱膨張率です。

このページでは、熱膨張率（線膨張率、体積膨張率）の意味と、長さの計算方法を紹介します。

熱膨張率とは

線膨張率とは？
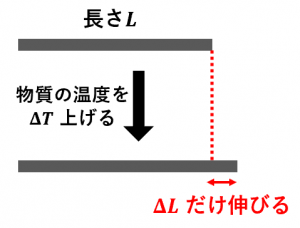
物質の温度を上げたときに、物質がどれくらい長くなるかを表す量です。
$L$ をもともとの物質の長さ、$\Delta T$ を上昇した温度の量、$\alpha$ を線膨張率とすると、
$\Delta L=\alpha L\Delta T$
という関係式が成立します。
線膨張率のことを、線膨張係数とも言います。

伸びた長さの計算

長さが2メートルのアルミニウムを10℃温めたときに、長さがいくら伸びるかを計算してみます。ただし、アルミニウムの線膨張率を $2.3\times 10^{-5}/\mathrm{K}$ とします。

線膨張率の公式：
$\Delta L=\alpha L\Delta T$
を使うと、伸びた長さは、
$\Delta L=2.3\times 10^{-5}\times 2\times 10\\
=4.6\times 10^{-4}\:\mathrm{m}$
つまり、$0.46\:\mathrm{mm}$ 伸びたと計算できます。

熱膨張率の単位

例えば「線膨張率が0.001毎ケルビン」というのは、1℃（1ケルビン）上げると、1メートルあたり長さが1mm伸びるという状況です。そんなに伸びる物質はなかなか無いです。

このように、熱膨張率は非常に $0$ に近い値になるので、$10^{-6}/\mathrm{K}$ という単位で表すことも多いです。「線膨張率が $10^{-6}/\mathrm{K}$」というのは、1℃（1ケルビン）上げると、1メートルあたり長さが0.001mm 伸びるという状況です。

体積膨張率とは

体積膨張率とは、物質の温度を上げたときに、物質の体積がどれくらい大きくなるかを表す量です。

$V$ をもともとの物質の体積、$\Delta T$ を上昇した温度の量、$\beta$ を体積膨張率とすると、
$\Delta V=\beta V\Delta T$
という関係式が成立します。
体積膨張率のことを、体積膨張係数とも言います。

線膨張率と体積膨張率の関係

立方体の物質の場合について、この関係式を導出してみます。

立方体では、$V=L^3$ です。また、熱膨張すると、
$V+\Delta V=(L+\Delta L)^3$
となります。$\Delta L$ が小さい場合には、$\Delta V\fallingdotseq 3L^2\Delta L$ が成立します。

これに、線膨張率と体積膨張率の公式：
$\Delta L=\alpha L\Delta T$
$\Delta V=\beta V\Delta T$
を代入すると、
$\beta V\Delta T\fallingdotseq 3L^3\alpha\Delta T$
つまり $\beta\fallingdotseq 3\alpha$ が成立します。

次回は 水温の計算（異なる温度の水の混合） を解説します。