正多角形の内角の大きさは、頂点の数を $n$ とすれば、
$\dfrac{180(n-2)}{n}$
という公式で計算できます。
正多角形の外角の大きさは、頂点の数を $n$ とすれば、
$\dfrac{360}{n}$
という公式で計算できます。
正多角形の内角と外角の大きさを計算する公式と計算例について詳しく解説します。
正三角形と正五角形の場合の具体例
例題:正三角形と正五角形の内角と外角の大きさをそれぞれ求めよ。
~内角~
正三角形の内角の大きさは、$\dfrac{180(n-2)}{n}$
という公式で $n=3$ とすると、
$\dfrac{180(3-2)}{3}=\dfrac{180}{3}=60^{\circ}$
正五角形の内角の大きさは、$n=5$ とすると、
$\dfrac{180(5-2)}{5}=\dfrac{540}{5}=108^{\circ}$

~外角~
正三角形の外角の大きさは、$\dfrac{360}{n}$ という公式で $n=3$ とすると、$\dfrac{360}{3}=120^{\circ}$
正五角形の外角の大きさは、$\dfrac{360}{5}=72^{\circ}$
正多角形の内角と外角の一覧表
| 図形 | 内角 | 外角 |
| 正三角形 | $60^{\circ}$ | $120^{\circ}$ |
| 正方形 | $90^{\circ}$ | $90^{\circ}$ |
| 正五角形 | $108^{\circ}$ | $72^{\circ}$ |
| 正六角形 | $120^{\circ}$ | $60^{\circ}$ |
| 正七角形 | 約 $129^{\circ}$ | 約 $51^{\circ}$ |
| 正八角形 | $135^{\circ}$ | $45^{\circ}$ |
内角の大きさの公式の説明
正多角形の内角の大きさが、
$\dfrac{180(n-2)}{n}$
という公式で計算できることを証明してみましょう。
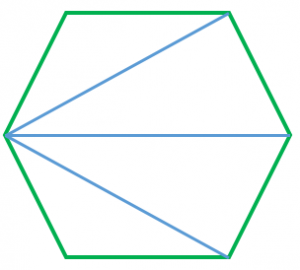
$n$ 角形は、三角形 $n-2$ 個に分割できます(例えば、六角形は四角形 $4$ 個に分割できる)。よって、$n$ 角形の内角の和は $180\times (n-2)$ 度になります。
正多角形の場合、内角の大きさは全て等しいので、一つの内角の大きさは、
$180(n-2)\div n=\dfrac{180(n-2)}{n}$ 度となります。
ちなみに、$n$ をどんどん増やしていくと、内角の大きさは大きくなっていき、しだいに $180^{\circ}$ に近づいていきます。
外角の大きさの公式の説明
正多角形の外角の大きさが、
$\dfrac{360}{n}$
という公式で計算できることを証明してみましょう。
公式の証明1
一般に多角形の外角の和は $360^{\circ}$ です。正 $n$ 角形の場合、外角の大きさは全て等しいので、一つの外角の大きさは $\dfrac{360}{n}$ 度となります。
公式の証明2
内角+外角 $=180^{\circ}$ なので、外角の大きさは、
$180-\dfrac{180(n-2)}{n}=\dfrac{360}{n}$ 度
ちなみに、$n$ をどんどん増やしていくと、外角の大きさは小さくなっていき、しだいに $0^{\circ}$ に近づいていきます。
次回は 三角柱の底面積、側面積、表面積の求め方 を解説します。
