- 元利均等返済(がんりきんとうへんさい)とは、毎回支払う金額が一定となるような返済方法です。
- 元金均等返済(がんきんきんとうへんさい)とは、毎回支払う金額のうち、元金の部分が一定となるような返済方法です。
元利均等返済と元金均等返済の例
元利均等返済の場合
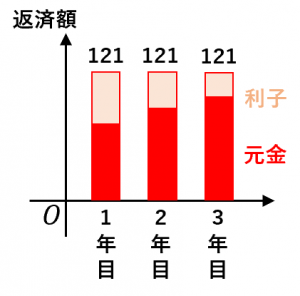
・1年目から3年目まで、毎年の返済額は同じで、およそ120万6千円になります。
・支払い総額はおよそ361万9千円になります。
元金均等返済の場合
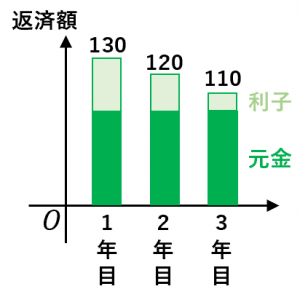
・1年目の返済額は130万円、2年目の返済額は120万円、3年目の返済額は110万円となります。
・支払い総額は360万円です。
元利均等返済と元金均等返済の比較
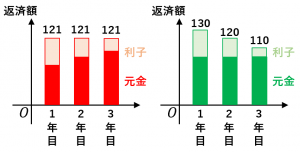
元利均等返済のメリット:
・支払い初期の負担が少ない
・支払額が一定なので分かりやすい
元金均等返済のメリット:
・支払い総額が少ない
・支払い末期の負担が少ない
支払期間が短い場合や、利子が低い場合には、両者の差は少ないです。一方、支払期間が長く、利子が高い場合には、上記のメリット・デメリットの効果が大きくなります。
元金均等返済の計算式
$\dfrac{A}{n}+A\left(1-\dfrac{k-1}{n}\right)r$
となります。
ただし、$A$ は元金(もともと借りた金額)、$r$ は利子、$n$ は返済回数です。
$\dfrac{A}{n}$ が元金の部分で、$A\left(1-\dfrac{k-1}{n}\right)r$ が利息の部分です。
元利均等返済の計算式
$x=\dfrac{Ar(1+r)^n}{(1+r)^n-1}$
ただし、$A$ は元金、$r$ は利子、$n$ は返済回数です。上の計算式を証明してみます。
毎回、利子によって残金が $(1+r)$ 倍され、$x$ だけ支払うので、1回目の返済後の残額は、
$A(1+r)-x$
2回目の返済後の残額は、
$A(1+r)^2-x(1+r)-x$
と計算できます。同様に、$n$ 回目の返済後の残金は、等比数列の和の公式を使うと、
$A(1+r)^n-x(1+r)^{n-1}-\dots -x\\
=A(1+r)^n-x\cdot\dfrac{(1+r)^n-1}{r}$
となります。よって、$n$ 回目で残額を $0$ にするための返済額は、
$x=\dfrac{Ar(1+r)^n}{(1+r)^n-1}$
となります。
年利と月利
今回紹介した2つの式:
$\dfrac{A}{n}+A\left(1-\dfrac{k-1}{n}\right)r$
$\dfrac{Ar(1+r)^n}{(1+r)^n-1}$
は、
・$r$ が年利で、$n$ が返済年数
・$r$ が月利で、$n$ が返済月数
のいずれの場合も使えます。
冒頭の「元利均等返済と元金均等返済の例」では前者の場合で計算しましたが、実際の住宅ローンなどでは、後者(月利計算で、月1回払い)の場合が多いです。
