二分法とは、方程式 $f(x)=0$ の解を数値的に計算する手法です。「解が存在する区間」の幅を繰り返し半分にしていくことで、方程式の解を探索します。
二分法とは
二分法は、$f(x)=0$ という方程式の解を計算する手法です。
$f(x)$ が連続関数であるときのみに使える手法です。以下では、$f(x)$ は連続関数とします。
性質:
$f(a)$ と $f(b)$ が異符号なら、$f(x)=0$ の解が $a$ と $b$ の間に存在する。
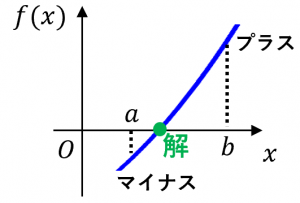
二分法では、この性質を繰り返し使って、区間の幅をどんどん狭くしていき、解が存在する場所を特定していきます。
二分法の具体的な手順
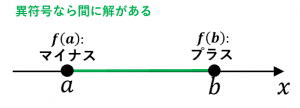
手順1. $f(a)$ と $f(b)$ が異符号である $a$ と $b$ を見つける
→性質により、$f(x)=0$ の解が $a$ と $b$ の間にあることが分かります。
手順2. 真ん中での関数の値を計算する
→$f(\frac{a+b}{2})$ がプラスなのか、マイナスなのかを調べます。
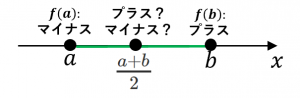
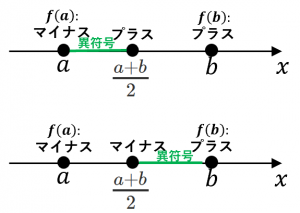
手順3. 左側半分か、右側半分のうち、$f$ の値が異符号になっている方を新しい区間とする
→$f(a)$ と $f(\frac{a+b}{2})$ が異符号なら、性質により、左側半分に解があります。
$f(b)$ と $f(\frac{a+b}{2})$ が異符号なら、性質により、右側半分に解があります。
どちらにしろ「解が存在する区間」の幅が半分になりました。
手順4. 手順2と3を繰り返す
→「解が存在する区間」の幅を、繰り返し半分にしていくことで、解の場所を特定していきます。
二分法の例:平方根を計算する
$\sqrt{2}$ は、$x^2-2=0$ の解です。つまり、$f(x)=x^2-2$ として二分法を適用してみましょう。
手順1. $f(a)$ と $f(b)$ が異符号である $a$ と $b$ を見つける
$f(1)=-1$、$f(2)=2$ です。$a=1$、$b=2$ とできます。
手順2. 真ん中での関数の値を計算する
$1$ と $2$ の真ん中は $1.5$ です。
$f(1.5)=0.25$ でプラスです。
手順3. 左側半分か、右側半分のうち、$f$ の値が異符号になっている方を新しい区間とする
$f(1)$ と $f(1.5)$ が異符号なので、左側半分、つまり「$1$ から $1.5$ の間」が新しい区間になります。
手順4. 手順2と3を繰り返す
・$1$ と $1.5$ の真ん中での関数の値は、$f(1.25)=-0.4375$ でマイナスです。
・$f(1.25)$ と $f(1.5)$ が異符号なので「$1.25$ から $1.5$ の間」が新しい区間になります。
・以下、同様に繰り返します。
少しの計算で、$\sqrt{2}$ が「$1.25$ から $1.5$ の間」にあることが分かりました(実際には、$\sqrt{2}=1.41421356\dots$ です)。「$1.25$ から $1.5$ の間」では大雑把過ぎますが、反復回数を増やしていけば、よりピンポイントに $\sqrt{2}$ の近似値を特定することができます。
同様に、$\sqrt{2}$ 以外の平方根も、二分法を使って計算することができます。
二分法の反復回数
・最初は区間の幅が $|b-a|$ です。
・1回手順2、3を行うと、区間の幅が $\dfrac{1}{2}|b-a|$ になります。
・$N$ 回反復を行うと、区間の幅が $\dfrac{1}{2^N}|b-a|$ になります。
よって、近似誤差を確実に $\varepsilon$ 以下にするためには、
$\dfrac{1}{2^N}|b-a|\leq\varepsilon$
を満たすような $N$ を求めて、$N$ 回反復すればOKです。
例えば「近似誤差 $10^{-6}$ 以内で計算したい、初期解の幅は $|b-a|=1$」という状況で必要な反復回数は、
$\dfrac{1}{2^N}\leq 10^{-6}$
をもとに求めると、$N\geq 20$ となります。
ニュートン法(二次収束)に比べて、二分法(一次収束)は収束が遅く、必要な反復回数が多めです。
次回は 速さと速度の違いと例 を解説します。
