単射:「単一のものから来る」ような関数のこと。
全射:「全部に行く」ような関数のこと。
単射、全射、全単射という数学用語について、定義と具体例を解説します。
なお、この記事では「関数」という言葉を使いますが、単射、全射の議論をするときには「写像」という言葉を同じ意味で使うことが多いです。
単射の意味
ここで「単一のものから来る」とは、どのような $y$ に対しても、$f(x)=y$ となるような $x$ が2つ以上は存在しないことを表します。
単射の例、単射でないものの例
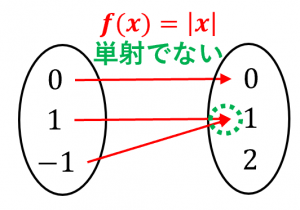
なぜなら、$y=1$ とすると、$f(x)=1$ となるような $x$ が $1$ と $-1$ で2つ存在するからです。
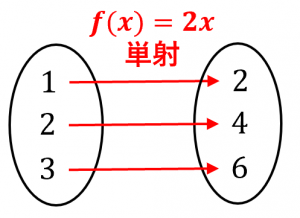
なぜなら、$f(x_1)=f(x_2)$ となるような相異なる $x_1,x_2$ が存在しないからです。「単一のものから来る」と言えます。
このように、単射の定義は、
「$f(x_1)=f(x_2)$ となるような相異なる $x_1,x_2$ が存在しない」
と言い換えることもできます。
全射の意味
ここで「全部に行く」とは、(予め定めた行き先の集合内の)どのような $y$ に対しても、$f(x)=y$ となるような $x$ が存在することを表します。
なお、全射のことを「上への写像」と言うこともあります。
全射の例、全射でないものの例
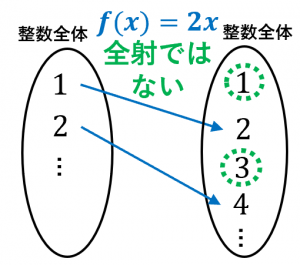
なぜなら、例えば $f(x)=1$ となるような $x$ が存在しないからです。「全部に行く」という性質は満たしません。
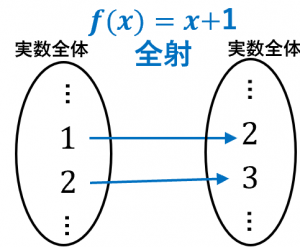
なぜなら、どのような実数 $y$ に対しても、$f(x)=y$ となる $x$ が、$x=y-1$ とすることで構成できるからです。「全部に行く」と言えます。
全単射とは
全単射は「単一のものから来る」かつ「全てに行く」ような関数です。
全単射は、2つの集合(定義域と終域)の間に1対1対応を定めます。つまり、全単射が存在する場合、定義域と終域は、ある意味で「同じサイズ」と考えることができます。(数学用語では、全単射が存在するような2つの集合は「濃度が同じ」と言います)
おわりに
数学では、いろいろな集合の間の対応関係(関数、写像)を考えることが多いです。単射、全射、全単射という言葉を使うと、対応関係の性質を簡潔に記述できます。
次回は 全単射と逆写像の存在についての2つの性質 を解説します。
