半減期とは、徐々に減っていくような量について「半分になるまでにかかる時間」のことです。
半減期の意味と、半減期に関する計算問題3問を解説します。
半減期とは
半減期の大雑把な意味:
半減期とは「半分になるまでにかかる時間」のことです。例えば、半減期が $t_0=3$ 年のものは、$3$ 年間経過すると量が半分になり、さらに $3$ 年間経過するともとの $\dfrac{1}{4}$ になります。
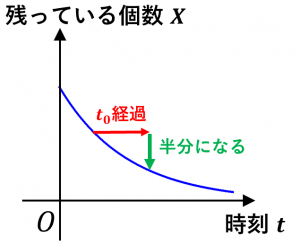
半減期の正確な定義:
より正確には、ある量 $X$ の時刻 $t$ での量が
$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$
という式に従うとき、$t_0$ のことを半減期と言います。
半減期の例:放射性元素
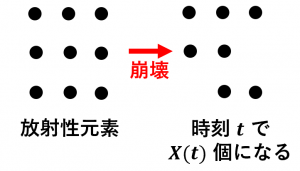
時刻 $t$ で崩壊せずに残っている原子の個数 $X(t)$ は、
$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$
という式で表されます。$X_0$ と $t_0$ は定数です。

どの時点についても、そこから時刻が $t_0$ だけ経過すると $X$ はちょうど半分になるので、$t_0$ のことを半減期と言います。
同様に、体内の薬の濃度なども上の赤い式で表現できる場合があり、その場合には $t_0$ のことを半減期と言います。
半減期を使った時間の計算
半減期に関する計算問題は、$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$ という式を使えば全て解けます。
$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$
において、$t_0=3$、$\dfrac{X(t)}{X_0}=\dfrac{1}{10}$ とすると、
$\left(\dfrac{1}{2}\right)^{\frac{t}{3}}=\dfrac{1}{10}$
となります。
両辺、2を底とする対数を取ると、
$-\dfrac{t}{3}=-\log_2 10$
となります。よって、$t=3\log_2 10$ となります。
$\log_2 10\fallingdotseq 3.32$ なので、$t\fallingdotseq 9.96$ 時間になります。
※例えば、Google の検索窓に「log2 10」と入力すると対数の計算ができます。
半減期そのものの計算
$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$
において $t=5$、$\dfrac{X(t)}{X_0}=\dfrac{1}{100}$ とすると、
$\dfrac{1}{100}=\left(\dfrac{1}{2}\right)^{\frac{5}{t_0}}$
となります。
両辺、2を底とする対数を取ると、
$-\log_2 100=-\dfrac{5}{t_0}$
$t_0=\dfrac{5}{\log_2 100}$
となります。対数を近似して計算すると、$t_0\fallingdotseq 0.752$ 年となります。
半減期を使った量の計算
$X(t)=X_0\left(\dfrac{1}{2}\right)^{\frac{t}{t_0}}$
において $t_0=2$、$X_0=1024$、$t=14$ とすると、
$X(14)=1024\cdot\left(\dfrac{1}{2}\right)^{7}=8$
となります。
次回は 指数関数の知識全5項目を整理(具体例からグラフまで) を解説します。
