最終更新日 2018/10/27
直角三角形の相似条件、および証明問題への応用について解説します。
直角三角形の相似条件
直角三角形の相似条件1（よく使う、重要）：
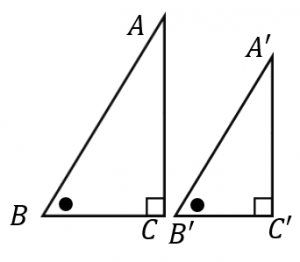
直角以外の角度一つが等しい。
つまり、
$\angle A=\angle A’$ または
$\angle B=\angle B’$
直角三角形の相似条件2（めったに使わない）：
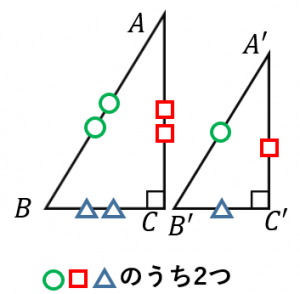
対応する2辺の比が等しい。
つまり、
$AB:A’B’=BC:B’C’$ または
$AB:A’B’=AC:A’C’$ または
$AC:A’C’=BC:B’C’$
証明問題への応用
例題
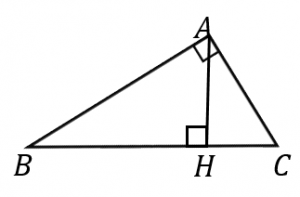
直角三角形 $ABC$ について、$A$ から下ろした垂線の足を $H$ とする。このとき、三角形 $ABC$ と $HBA$ が相似であることを証明せよ。
解答
三角形 $ABC$ と $HBA$ はいずれも直角三角形です。そして、$\angle B$ を共通に持ちます。よって、これらの三角形は直角以外の角度一つが等しい直角三角形なので、直角三角形の相似条件1より相似であることが証明されました。
補足：このように、2つの直角三角形が相似であることを示すときには、もう一組等しい角度を探しましょう（辺の比が等しいことを用いて相似を証明する問題はあまり出題されません）。
相似条件が正しいことの説明
直角三角形の相似条件は、一般の三角形の相似条件に帰着することで説明できます。
相似条件1の説明
相似条件1が成立する
→二つの角度が等しい
→一般の三角形の相似条件「2つの角度が等しい三角形は相似」が使える
相似条件2の説明
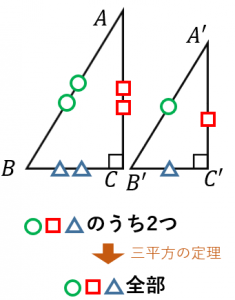
相似条件2が成立する
→（三平方の定理より）残り1組の辺の比も等しい
→一般の三角形の相似条件「3つの辺の比がそれぞれ等しい三角形は相似」が使える
次回は 直角二等辺三角形の辺の長さの求め方 を解説します。
