2点 $A(x_1,y_1)$、$B(x_2,y_2)$ の中点の座標は、$\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)$
例題2問
(1):$A(2,3)$、$B(4,1)$ の中点の座標を求めよ。
解答:中点の座標は、冒頭の公式より、
$\left(\dfrac{2+4}{2},\dfrac{3+1}{2}\right)=(3,2)$
(2):$A(-1,3)$、と $B(a,b)$ の中点の座標が $(0,1)$ であるとき、$a$ と $b$ を求めよ。
解答:線分 $AB$ の中点の座標は、冒頭の公式より、
$\left(\dfrac{-1+a}{2},\dfrac{3+b}{2}\right)$
これが $(0,1)$ と等しいので、
$\dfrac{-1+a}{2}=0$
$\dfrac{3+b}{2}=1$
よって、この方程式を解くと、$a=1,b=-1$
公式の証明
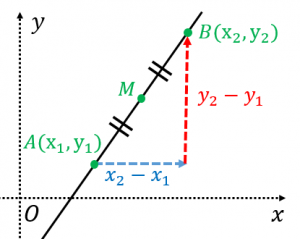
$AB$ の中点を $M$ とします。$A$ から右に $(x_2-x_1)$ だけ進んで、上に $(y_2-y_1)$ だけ進むと $B$ にたどりつきます(図参照)。
「$A$ から $M$ への移動」は「$A$ から $B$ への移動」の半分なので、
$A$ から右に $\frac{1}{2}(x_2-x_1)$ だけ進んで、上に $\frac{1}{2}(y_2-y_1)$ だけ進むと $M$ にたどりつきます。
つまり、$M$ の $x$ 座標は、
$x_1+\frac{1}{2}(x_2-x_1)=\frac{x_1+x_2}{2}$
となります。同様に、$M$ の $y$ 座標は、
$y_1+\frac{1}{2}(y_2-y_1)=\frac{y_1+y_2}{2}$
となります。
座標空間上で中点を求める公式
上記で解説した公式は中学数学で習います。
これを発展させた公式に、三次元座標空間上で中点の座標を求める公式があります(高校数学で習います)。
座標空間上において、
$A(x_1,y_1,z_1)$、$B(x_2,y_2,z_2)$ の中点の座標は、$\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2},\dfrac{z_1+z_2}{2}\right)$
同じく各成分について平均を計算するという形の公式になっています。
次回は 二点間の距離を求める公式(2次元、3次元) を解説します。
