極座標における円の方程式の一般形と例題

極座標平面における円の方程式について詳しく解説します。

中心が原点の場合の円の極方程式

中心が原点で、半径が $R$ であるような円の方程式は、極座標では、
$r=R$
と表すことができます。

$xy$ 直交座標平面での $x^2+y^2=R^2$ という式よりも簡潔で分かりやすいです。

一般の場合の円の方程式

中心が $(r_0,\theta_0)$ で、半径が $R$ であるような円の方程式を極座標で表すと、
$r^2+r_0^2-2r_0r\cos(\theta-\theta_0)=R^2$
となります（証明は後ほど）。

特に、$R=r_0$ である場合（つまり、円が原点を通る場合）は、
$r=2r_0\cos(\theta-\theta_0)$
のように簡潔な式になります。

ちなみに、この式は、磁場中の荷電粒子の運動を解析する際に役に立ったりします。
参考：Kaggle（trackmlコンペ）

例題

三角関数の合成公式を使うと、右辺は、
$-3\sin\theta+3\sqrt{3}\cos\theta\\
=6\sin\left(\theta+\dfrac{2}{3}\pi\right)$
となります。さらに、$\sin\left(\theta+\dfrac{\pi}{2}\right)=\cos\theta$
であることを使うと、与えられた極方程式は
$r=6\cos\left(\theta-\dfrac{\pi}{6}\right)$
と変形できます。

これは、半径が $6\div 2=3$ で、中心が $\left(3,\dfrac{\pi}{6}\right)$ であるような円の方程式です。

余弦定理を使った証明

円の極方程式：
$r^2+r_0^2-2r_0r\cos(\theta-\theta_0)=R^2$
を２通りの方法で導出してみます。

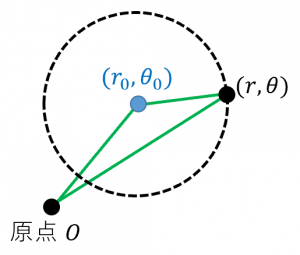
$(r,\theta)$ という点が、所望の円の上にある条件は、緑色の三角形に余弦定理を使うと、
$r^2+r_0^2-2rr_0\cos|\theta-\theta_0|=R^2$
となります。$\cos x=\cos(-x)$ なので、絶対値が外せて、
$r^2+r_0^2-2r_0r\cos(\theta-\theta_0)=R^2$
が求める円の極方程式となります。

直交座標から証明

中心が $(r_0,\theta_0)$ で半径が $R$ である円の方程式を直交座標で表すと、
$(x-r_0\cos\theta_0)^2+(y-r_0\sin\theta_0)^2=R^2$
となります。

$x^2+y^2=r^2$、$x=r\cos\theta$、$y=r\sin\theta$ に注意して左辺を変形していくと、
$r^2-2r_0(x\cos\theta_0+y\sin\theta_0)+r_0^2\\
=r^2-2rr_0(\cos\theta\cos\theta_0+\sin\theta\sin\theta_0)\\
=r^2-2rr_0\cos(\theta-\theta_0)$
となります。

次回は 円に内接する四角形の面積を求める公式 を解説します。