相関係数(ピアソンの積率相関係数):
$\dfrac{\displaystyle\sum_{i=1}^n(x_i-\mu_x)(y_i-\mu_y)}{\sqrt{\displaystyle\sum_{i=1}^n(x_i-\mu_x)^2}\sqrt{\displaystyle\sum_{i=1}^n(y_i-\mu_y)^2}}$
二つの量の関係性を表す量。
(ただし、$x_i,y_i$ はデータで、$\mu_x,\mu_y$ はそれらの平均)
数式は難しく見えますが、実際に計算してみると、そこまで難しくないということが分かります。
問題設定(状況)
二組のデータ:
$x_1,x_2,\cdots,x_n$
$y_1,y_2,\cdots,y_n$
が与えられた状況を考えます。
例:4人の数学の点数 $x_i$ と物理の点数 $y_i$
A君、$x_1=100$、$y_1=90$
B君、$x_2=80$、$y_2=80$
C君、$x_3=70$、$y_3=60$
D君、$x_4=70$、$y_4=50$
数学の点数と物理の点数には相関がありそう(数学の点数がよいほど物理の点数もよいという関係がありそう)ですね。
記事の後半で、この例題について、具体的に相関係数を計算してみます。その前に、相関係数の意味について説明します。
相関係数の意味
相関係数は $-1$ 以上 $1$ 以下の値を取ることが知られています。さらに、以下が成立します:
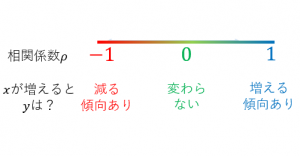
相関係数が $1$ に近い
$\iff$ $x$ が増えると $y$ が増える傾向にある
($x$ と $y$ には正の相関がある)
相関係数が $-1$ に近い
$\iff$ $x$ が増えると $y$ が減る傾向にある
($x$ と $y$ には負の相関がある)
相関係数が $0$ に近い
$\iff$ $x$ が増えても $y$ の値はあまり変わらない
($x$ と $y$ は無相関)
相関係数の具体的な求め方
上記の具体例について、実際に相関係数
$\dfrac{\displaystyle\sum_{i=1}^4(x_i-\mu_x)(y_i-\mu_y)}{\sqrt{\displaystyle\sum_{i=1}^4(x_i-\mu_x)^2}\sqrt{\displaystyle\sum_{i=1}^4(y_i-\mu_y)^2}}$
を計算してみます。
手順1:平均 $\mu_x$、$\mu_y$ を求める。
数学の平均点は、
$\mu_x=\dfrac{100+80+70+70}{4}=80$
物理の平均点は、
$\mu_y=\dfrac{90+80+60+50}{4}=70$
→平均の求め方(計算式)と意味、欠点
手順2:それぞれの平均からのズレの二乗和を求める。
相関係数の分母(のルートの中身)を計算します。
数学は、
$\sum_{i=1}^4(x_i-80)^2\\
=\{20^2+0^2+(-10)^2+(-10)^2\}\\
=600$
物理は、
$\sum_{i=1}^4(y_i-70)^2\\
=\{20^2+10^2+(-10)^2+(-20)^2\}\\
=1000$
手順3:相関係数の分子(偏差積)を求める。
$\sum_{i=1}^4(x_i-\mu_x)(y_i-\mu_y)\\
=\{20\cdot 20+(-10)(-10)+(-10)(-20)\}\\
=700$
手順4:手順2、3の結果をもとに相関係数を計算する。
$\rho=\dfrac{700}{\sqrt{600}\cdot\sqrt{1000}}\\
=\dfrac{7}{\sqrt{60}}\\
\simeq 0.90$
相関係数が $1$ に近いので「数学の点数が高い人ほど物理の点数も高い傾向にある」と結論づけることができます。
次回は 坂道の勾配に関する計算(角度、高さ、水平距離などの関係) を解説します。
