ヒンジ関数について紹介します。
ヒンジ関数とは
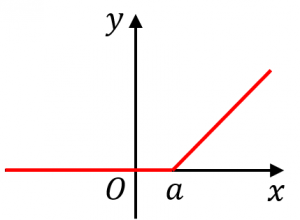
例えば、赤いグラフの関数を式で表すと、
$f(x)=\begin{cases}0&(x\leq a)\\x-a&(x>a)\end{cases}$
のようになります。
2つの式をまとめて
$f(x)=\max(0,x-a)$
と書くこともできます。
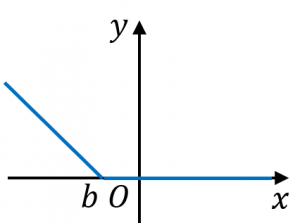
別の例として、青いグラフの関数を式で表すと、
$f(x)=\begin{cases}b-x&(x\leq b)\\0&(x>b)\end{cases}$
のようになります。
2つの式をまとめて
$f(x)=\max(0,b-x)$
と書くこともできます。
ヒンジ関数の活用例
逆に、これ以外の場面でヒンジ関数が登場することはほとんどないような気がします。
そこで、以下では SVM におけるヒンジ関数の役割について(大雑把なイメージレベルで)説明します。
SVM の問題設定
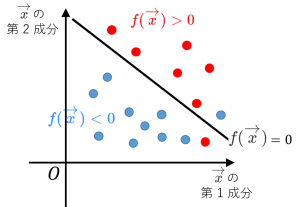
SVMでは、
・クラスを判別するための線形関数 $f(\overrightarrow{x})=\overrightarrow{w}^{\top}\overrightarrow{x}+b$ を求めます($\overrightarrow{x}$ は説明変数です。$\overrightarrow{w}$ と $b$ を求めます)。
・$f(\overrightarrow{x})>0$ ならクラス1と判定し、$f(\overrightarrow{x})<0$ ならクラス2と判定します。
ヒンジ関数が使えそうであることの説明
SVM では、ヒンジ形の関数の、各データ点についての和
$E=\displaystyle\sum_{i}\max(0,1-y_if(\overrightarrow{x_i}))$
を小さくするような $f$ を探します(※)。
実際、以下の説明1~3から分かるように、$E$ はそれっぽい損失関数になっています($E$ が小さいほど正しく判別できている、とみなせそう)。
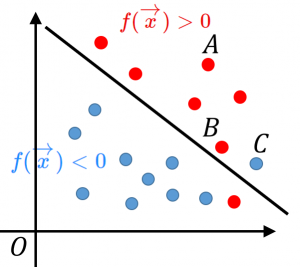
点Aのように、正しく判別され、しかも境界面から遠い点の損失は0。
実際、この場合、$y_i$ と $f(\overrightarrow{x_i})$ は同符号です。そして、データは境界面から遠いので、$f(\overrightarrow{x_i})$ の絶対値は大きくなります。よって、$y_if(\overrightarrow{x_i})\geq 1$ となり、ヒンジ関数の値は $0$ になります。
点Bのように、正しく判別できても境界面に近い点(ギリギリ判別できたけど危うく間違えそうだった点)では、少しの損失。
実際、この場合、$y_i$ と $f(\overrightarrow{x_i})$ は同符号ですが、データは境界面に近いので、$f(\overrightarrow{x_i})$ の絶対値は小さくなります。よって、$0< y_if(\overrightarrow{x_i})< 1$ となり、ヒンジ関数の値は $0$ に近い正の数になります。
点Cのように誤判別してしまったデータでは、1より大きい損失。境界面から遠くなればなるほど、損失の値は大きくなる。
実際、この場合、$y_i$ と $f(\overrightarrow{x_i})$ は異符号です。$y_if(\overrightarrow{x_i})< 0$ となり、ヒンジ関数の値は $1$ より大きくなります。
※より正確には $E+\lambda\|\overrightarrow{w}\|_2$ を最小化するような関数を探します。
(参考文献:パターン認識と機械学習(下),C.M.ビショップ著 7.1節)
次回は 誤差伝播の公式の意味と証明 を解説します。
