最終更新日 2018/02/05
・$a:b$ に分ける問題
・比から個数を求める問題
の計算方法をそれぞれ説明します。
$a:b$ に分ける問題
$48$ 個のみかんを $5:3$ に配分すると、いくつといくつになるか計算してみましょう。
$5:3$ に分けるために、まずは $5+3=8$ グループに分けます。
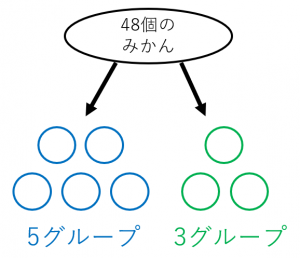
このとき、1グループには、$48\div 8=6$ 個のみかんがあります。
全体を $5:3$ に分けるのは、$8$ つのグループを $5$ つのグループと $3$ つのグループに分けることに対応します。
よって、
$5$ つのグループには、みかんが $6\times 5=30$ 個
$3$ つのグループには、みかんが $6\times 3=18$ 個
になります。
つまり、$48$ 個を $5:3$ に分けると、$30$ 個と $18$ 個になります。
$a:b$ に分ける問題のポイント
上の解答のポイントをおさらいします。
$a:b$ に分けたいときは、
まず、全体の個数を $a+b$ で割って、1グループの個数を求めます。
そして、
1グループの個数に $a$ をかけたものと
1グループの個数に $b$ をかけたもの
が分けた後の個数になります。
比から個数を求める問題
いくつかのりんごを、$A$ さんと $B$ さんに、$2:3$ の比率で分けました。$A$ さんがもらったりんごが $8$ 個のとき、$B$ さんがもらったりんごはいくつでしょうか?

解答
2グループぶんのりんごが $8$ 個ということは、
1グループぶんのりんごは、$8\div 2=4$ 個です。
$B$ さんは3グループぶんのりんごをもらっているので、$4\times 3=12$ 個もらったことになります。
まとめ
・比率(何対何)に関する計算問題にはいくつかタイプがあります。
・多くの場合、1グループぶんが何個なのか?を考えることで計算することができます。
・3つ以上の比率の場合(連比の問題)については、下記リンク先で解説しています。
次回は 連比を計算する2通りの方法と例題 を解説します。
