1からnまでの和を求める公式

具体例で学ぶ数学 > 計算 > 1からnまでの和を求める公式

最終更新日 2019/05/12

$1+2+3+\cdots +n=\dfrac{1}{2}n(n+1)$

1からnまでの和を求める公式について、具体例と２通りの証明を解説します。

具体例

・$1$ から $10$ までの和
$1+2+3+\cdots +9+10\\
=\dfrac{1}{2}\times 10\times 11=55$

・$1$ から $100$ までの和
$1+2+3+\cdots +99+100\\
=\dfrac{1}{2}\times 100\times 101=5050$

・$1$ から $1000$ までの和
$1+2+3+\cdots +999+1000\\
=\dfrac{1}{2}\times 1000\times 1001=500500$

公式を使えばいちいち１つずつ足し算を計算する必要がないので楽です。

なぜ $1+2+3+\cdots +n=\dfrac{1}{2}n(n+1)$ が成立するのか説明します。

まずは $n=10$ の場合について考えてみましょう。

(求めたいもの)$=1+2+3+\cdots +10$
(求めたいもの)$=10+9+8+\cdots +1$

この2つの式を縦に足すと、
$2\times$(求めたいもの)
$=(1+10)+(2+9)+(3+8)+\cdots +(10+1)$

となります。この右辺は、
$11+11+11+\cdots +11$
となり、$11$ が $10$ 個です。

よって、
(求めたいもの)$=11\times 10\div 2$
となります。

同様の方法を使うと、$n$ が $10$ ではない別の自然数の場合にも、
$1+2+\cdots +n=(n+1)\times n\div 2$
つまり
$1+2+\cdots +n=\dfrac{1}{2}n(n+1)$
となります。

ちなみに、この公式を和の記号 $\Sigma$ を使って書くと、
$\displaystyle\sum_{k=1}^na_k=\dfrac{1}{2}n(n+1)$
となります。

今度は図形を使って、なぜ
$1+2+3+\cdots +n=\dfrac{1}{2}n(n+1)$
が成立するのか説明します。

同じく $n=10$ の場合について考えてみましょう。

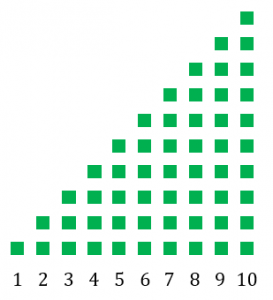
求めたいものは $1+2+3+\cdots +10$
つまり、緑色の四角形の個数です。

そこで、緑色全体をひっくり返したもの（赤色）を上側にくっつけてみましょう。

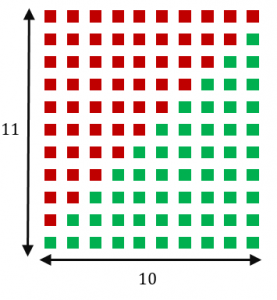
すると、赤＋緑
は合計 $10\times 11$ 個です。

よって、緑はその半分の $\dfrac{1}{2}\times 10\times 11$ 個になります。

同様に、$n$ が $10$ ではない別の自然数の場合にも、
$1+2+\cdots +n=(n+1)\times n\div 2$
であることが分かります。