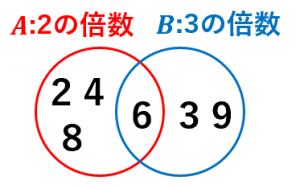
ベン図とは、複数の集合の関係を図として表した上図のようなものです。英語では、Venn diagram と言います。
このページでは、ベン図について、
・ベン図とは何か?
・ベン図における共通部分・和集合とは?
・ベン図を使った問題を解く方法は?
といった疑問にお答えします。
ベン図とは
例えば、1から9までの範囲で、
$A$ を2の倍数の集合
$B$ を3の倍数の集合
としてみます。このとき、ベン図は図のようになります。

集合 $A$ が左の円に対応し、集合 $B$ が右の円に対応します。このように、2つの集合の関係を表すベン図では、2つの円を交わるように書きます。
ベン図といろいろな集合
ベン図における共通部分
ベン図において、2つの円が重なる部分は
「$A$ と $B$ の両方ともに属する要素」
に対応します。
このような要素を集めた集合を共通部分と言い、$A\cap B$ という記号で表します。
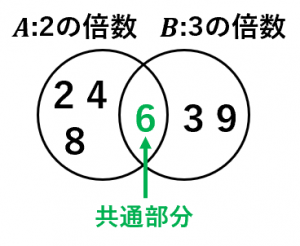
例えば、さきほどの例では $6$ は $2$ の倍数かつ $3$ の倍数なので、共通部分の要素になります。
ベン図における和集合
ベン図において、2つの円のどちらかに属する部分は
「$A$ と $B$ の少なくとも1つには属する要素」
に対応します。
このような要素を集めた集合を和集合と言い、$A\cup B$ という記号で表します。
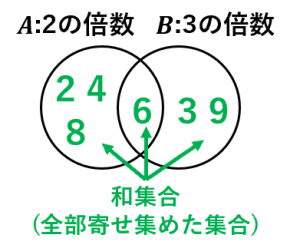
例えば、さきほどの例では和集合は、
$A\cup B=\{2,3,4,6,8,9\}$
になります。
ベン図を使った問題の例
ベン図に慣れるために、ベン図を使った問題を解いてみましょう。
まずは、ベン図を書いてみましょう。
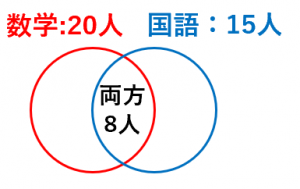
「数学が得意だけど、国語は苦手な人」の人数は、$20-8=12$
「国語が得意だけど、数学は苦手な人」の人数は $15-8=7$
です。これをベン図に書き込んでみます。
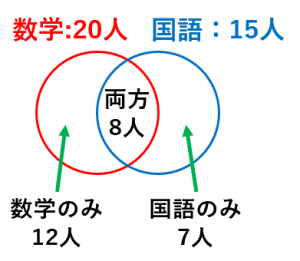
よって、
「数学か国語の少なくとも1つは得意な人」の人数は、
$12+8+7=27$
となります。
3つの集合のベン図
2つの集合の関係を表すベン図は「2つの円」で表現できました。
同様に、3つの集合の関係を表すベン図は「3つの円」で表現されます。
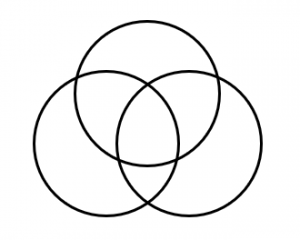
一般的には、図のように、それぞれが重なり合う3つの円で表現される場合が多いです。3つの集合の共通部分が存在しない場合は、重なる部分がないような図になることもあります。
次回は 和集合と積集合の意味と公式 を解説します。
