VC次元(Vapnik-–Chervonenkis Dimension)について解説します。
VC次元の概要
2クラス分類問題について、分類器 $f$ の集合 $F$ を考えます。ここで、分類器とは、データ $x_i$ を入力すると $1$ または $-1$ を出力する関数とします。
VC次元は、$F$ に対して定まる $0$ 以上の整数(または $+\infty$)で、ある意味で「$F$ の大きさ」を表します。
例えば、入力データを2次元平面上の点とし、$F$ を線形分類器全体の集合(つまり、直線の片側にあれば $1$ を出力し、反対側にあれば $-1$ を出力する関数)とします。このとき、$F$ のVC次元は $3$ になります。(詳細は後述します)
一般に、
VC次元が大きい → $F$ は広い → 訓練誤差は下がりやすいが、過学習しやすい
VC次元が小さい → $F$ は狭い → 訓練誤差を下げるのは大変だが、過学習しにくい
という傾向があると考えられそうです。
VC次元の定義
以下の性質が成り立つ最大の $n$ を $F$ のVC次元と言います。
性質:
ある $n$ 個のデータが存在して「そのデータのすべての($2^n$ 通りある)ラベル付けに対して、完璧に分類する分類器 $f$ が $F$ に存在する」
VC次元の具体例
まず、$n=3$ の場合に「性質」が成立することを確認します。
平面上の「一直線上にない3つの点」を適当にとってきます。これらの3つの点のラベル付けは8通りありますが、いずれの場合もうまく直線を引けば、完璧に分類できます。
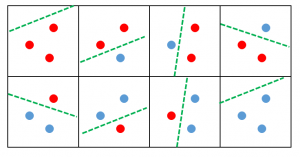
次に、$n=4$ の場合に「性質」が成立しないことを確認します。
4個のデータが与えられたときを考えます。
・4つの点の凸包が四角形をなす場合、図のような「交互の」ラベル付けに対して完璧に分類する直線は引けません。
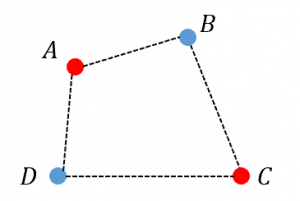
($A$ と $C$ をうまく分類できていれば、対角線の交点は赤色になるはず。$B$ と $D$ をうまく分類できていれば、対角線の交点は青色になるはず。両方を満たすことはできない。)
・4つの点の凸包が三角形をなす場合、図のような「頂点でないものが仲間はずれ」のラベル付けに対して完璧に分類する直線は引けません。
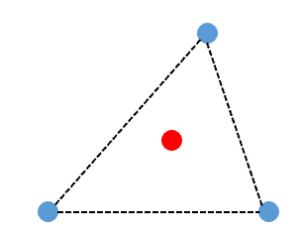
・4つの点の凸包が直線の場合、図のような「交互の」ラベル付けに対して完璧に分類する直線は引けません。
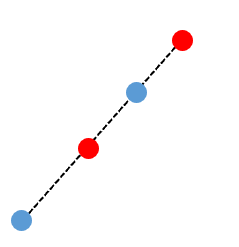
つまり、どんな $4$ 個のデータに対しても「そのデータに対するあるラベル付けに対して、完璧に分類する分類器 $f$ は $F$ に存在しない」となるので、$n=4$ の場合に「性質」は成立しません。
余談
VC次元は、PAC学習の理論を仮説集合が有限でない場合にも拡張する際に、登場する指標です。
次回は ピンスカーの不等式(Pinsker’s Inequality) を解説します。
