最小公倍数の２通りの求め方（3つの場合も）

最小公倍数の意味と、最小公倍数を求める２つの方法を解説します。また、３つの数の最小公倍数の求め方も紹介します。

最小公倍数とは

$4$ と $6$ の最小公倍数は $12$ です。

実際、$12$ は $12=4\times 3$ なので $4$ の倍数であり、$12=6\times 2$ なので $6$ の倍数でもあります（$4$ と $6$ の公倍数）。また、$4$ と $6$ の公倍数で $12$ より小さいものはありません。

最小公倍数の求め方１：全て列挙

$18$ の倍数は $18,36,54,72,90,108,\cdots$
$24$ の倍数は $24,48,72,96,120,\cdots$
最小公倍数（＝両方ともに登場する最小の数）は、$72$

最小公倍数の求め方２：わり算

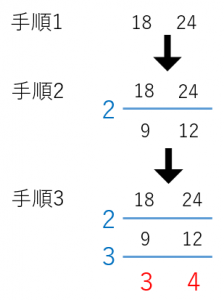
手順1. 最小公倍数を求めたい二つの数字を並べる
手順2. 両方ともでわり切れる数を左に書いて、実際にその数でわる（今回は $2$ でわれる）
手順3. 手順2をできるだけ繰り返す（今回は、さらに $3$ でわれる）
手順4. 左と下に並んだ数字（青い数字と赤い数字）をかけ算すると求めたい最小公倍数になる

答えは、$2\times 3\times 3\times 4=$$72$

３つの数の最小公倍数とは

今までは、２つの数の最小公倍数について考えてきました。

同様に、$3$ つ以上の数字についても、全てのものの倍数を公倍数と言い、公倍数の中で一番小さいものを最小公倍数と言います。
例えば $4$ と $6$ と $8$ の最小公倍数は、$24$ です（求め方は後述します）。

３つの数の最小公倍数の求め方

方法１：全て列挙

それぞれの倍数を全部書いていく：
$4$ の倍数は、$4,8,12,16,20,24,28,32,\cdots$
$6$ の倍数は、$6,12,18,24,30,36,\cdots$
$8$ の倍数は、$8,16,24,32,40,\cdots$
全部に共通するもの（の中で一番小さいもの）は $24$ です。

方法２：わり算

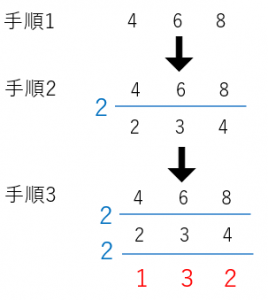
こちらの方法は手順2（および3）が少し変わります。

「両方ともでわり切れる数を左に書いて、実際にその数でわる」ではなくて、
「2つ以上でわり切れる数を左に書いて、わりきれるものだけ、実際にその数でわる」に変わります。

答えは、$2\times 2\times 1\times 3\times 2=$$24$

次回は 最大公約数：求め方、3つの場合 を解説します。