最大値と極大値の違いと英語

最大と極大の違い

考えている区間の中で一番大きいのが最大、自分の近所に限定すれば一番大きいのが極大です。図を見て覚えましょう。

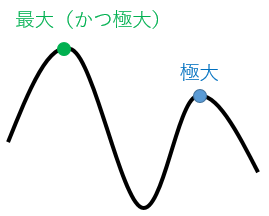
ちなみに、全体で一番大きいところは、自分の近所に限定しても一番大きいので、最大値は極大値でもあります。逆に、近所で一番でも世界一とは限らないので、極大でも最大とならないことはあります。

同様に、考えている区間の中で一番小さいのが最小、自分の近所に限定すれば一番小さいのが極小です。

英語

最大値：maximum value, global maximum
極大値：maximul value, local maximum

最小値：minimum value, global minimum
極小値：minimul value, local minimum

global というのが全体の中で一番強い、local が自分の近所では一番強い、という状況を表現しています。mul と mum　を使い分けるよりも、global と local を使う方が分かりやすい気がします。

余談：何かで世界一になるのは大変ですが、近所で一番になるのは簡単です。人生においても、とりあえずは極大を目指しましょう。

極値と微分

極大値と極小値をあわせて極値と言います。

（$f(x)$ が微分可能なもと）
関数 $f(x)$ が $x=a$ で極値を取るなら、$f'(a)=0$
が成立します。

よって、極値を求めたいときは、$f(x)$ を微分して $0$ になる点を探すことになります。ただし、微分できない関数もあり、この方法で全ての極値を見つけられるわけではありません。

余談：定数関数は全ての点が、最大かつ最小（かつ極大かつ極小）となります。世界中探しても自分より大きい点も小さい点も存在しないからです。

次回は 漸近線の求め方３パターン を解説します。