関数 $f(x)$ がリプシッツ連続であるとは、
任意の $x_1,x_2$ に対して
$|f(x_1)-f(x_2)|\leq k|x_1-x_2|$
を満たすような定数 $k$ が存在することを言います。
リプシッツ連続とは、関数の連続性に関する概念です。リプシッツ連続の意味や、リプシッツ連続、一様連続、(普通の)連続の関係などを解説します。
リプシッツ連続の意味
・$|f(x_1)-f(x_2)|\leq k|x_1-x_2|$ となる定数 $k$ が存在する
・関数上のどの点でも、傾き $\pm k$ の直線を引くと、関数のグラフはその間におさまっている
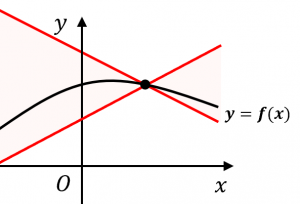
・2点間の距離が、$f$ を作用させることで $k$ 倍より大きくはならない
ちなみに、リプシッツ連続は英語で Lipschitz continuity と言います。
リプシッツ連続と一様連続、普通の連続
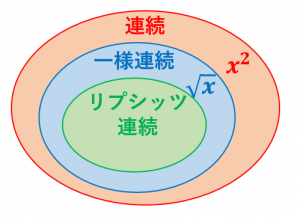
1. リプシッツ連続なら一様連続
2. 一様連続なら(普通の)連続
3. 一様連続だがリプシッツ連続ではない関数がある
4. 連続だが一様連続ではない関数がある
1~4の証明は後述します。まずは普通の連続と一様連続の定義を復習します。
普通の連続:
$x=x_0$ で連続とは、
$\displaystyle\lim_{x\to x_0}f(x)=f(x_0)$
が成立することを言います。また、考えている区間の全ての点で連続であるとき、$f(x)$ は連続関数であると言います。
一様連続:
関数 $f(x)$ が一様連続とは、
任意の $\varepsilon > 0$ に対して、ある $\delta >0$ が存在して、
$|x_1-x_2|<\delta$ なら $|f(x_1)-f(x_2)|<\epsilon$
が成立することを言います。
リプシッツ連続:
関数 $f(x)$ がリプシッツ連続であるとは、
任意の $x_1,x_2$ に対して
$|f(x_1)-f(x_2)|\leq k|x_1-x_2|$
を満たすような定数 $k$ が存在することを言います。
リプシッツ連続と他の連続性の関係の証明
1. リプシッツ連続なら一様連続
証明してみます。リプシッツ連続のとき、
任意の $\varepsilon >0$ に対して $\delta=\dfrac{\varepsilon}{k}$ とおくと、
$|x_1-x_2|<\delta$ なら $|f(x_1)-f(x_2)|<\varepsilon$
となります。つまり、$f(x)$ は一様連続になります。
※$k$ はリプシッツ連続の定義に現れる定数です。$k=0$ の場合は、$\delta=\dfrac{\varepsilon}{k}$ とおけませんが、この場合には $f(x_1)=f(x_2)$、つまり定数関数になるので、$f(x)$ は一様連続です。
2. 一様連続なら連続
一様連続の方が連続よりも強い定義なので明らかです。
3. 一様連続だがリプシッツ連続ではない関数がある
$f(x)=\sqrt{x}\:(x\geq 0)$ はリプシッツ連続ではありません。
実際、
$\sqrt{x}-0\leq k|x-0|$
を成立させるためには $k\geq\dfrac{1}{\sqrt{x}}$
である必要がありますが、どのような定数 $k$ を持ってきても、$x$ を限りなく $0$ に近づけると、上の不等式は成立しません。
$f(x)=\sqrt{x}\:(x\geq 0)$ は一様連続です。
実際、任意の $\varepsilon > 0$ に対して、$\delta=\varepsilon^2$ とすれば
$|x_1-x_2|<\delta$ なら
$|\sqrt{x_1}-\sqrt{x_2}|\\
=\dfrac{|x_1-x_2|}{\sqrt{x_1}+\sqrt{x_2}}\\
<\dfrac{\delta}{\sqrt{\delta}}=\epsilon$
4. 連続だが一様連続ではない関数がある
実際、$y=x^2$ は連続ですが一様連続ではありません。確認してみてください。
次回は 劣勾配と劣微分の定義と意味 を解説します。
