長さが等しい2つの $n$ 次元ベクトル $x,y$ が与えられたとします。また、$u=x-y$ とおきます。このとき、
$P=I-\dfrac{2uu^{\top}}{\|u\|^2}$
という行列をハウスホルダー行列と言います。
ハウスホルダー変換
ハウスホルダー変換は、$x$ と $y$ を交換するような鏡映変換になります。
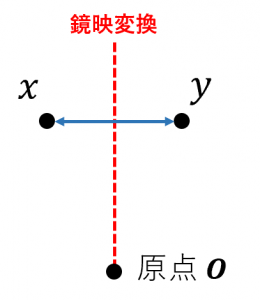
これを確認してみます。
任意のベクトル $z$ に対して、ハウスホルダー変換したベクトルは、
$Pz=z-2\dfrac{uu^{\top}}{\|u\|^2}z\\
=z-\dfrac{2u^{\top}z}{\|u\|}\dfrac{u}{\|u\|}$
となります。
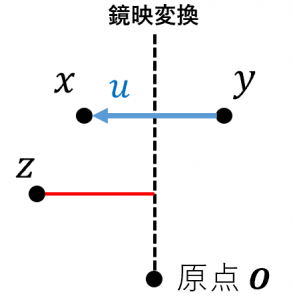
この第二項は、$u$ 方向の単位ベクトルの $-\dfrac{2u^{\top}z}{\|u\|}$ 倍であり、$\dfrac{u^{\top}z}{\|u\|}$ は図の赤い線の長さに対応するので、ハウスホルダー変換は確かに鏡映です。
また、$Px=y$ および $Py=x$ も簡単な計算で確認できます。
対称行列であること
これは、簡単な式変形で証明できます。
$P^{\top}=I^{\top}-\left(\dfrac{2uu^{\top}}{\|u\|^2}\right)^{\top}\\
=I-\dfrac{2uu^{\top}}{\|u\|^2}\\
=P$
となります。
直交行列であること
これを証明してみましょう。まず、$P$ は対称行列なので、$P^{\top}=P$ です。よって、
$P^{\top}P=P^2\\
=\left\{I-\dfrac{2uu^{\top}}{\|u\|^2}\right\}^2\\
=I-\dfrac{2uu^{\top}}{\|u\|^2}-\dfrac{2uu^{\top}}{\|u\|^2}+\dfrac{4uu^{\top}uu^{\top}}{\|u\|^4}\\
=I$
となります。最後の式変形で $u^{\top}u=\|u\|^2$ を使いました。
固有値1を持つこと
鏡映変換においては、折返しライン(垂直二等分線)上の点は変換によって変わらないので、$\dfrac{x+y}{2}$ が固有値1の固有ベクトルであることが分かります。
一応計算でも確認してみます:
$P(x+y)\\
=(x+y)-\dfrac{2uu^{\top}}{\|u\|^2}(x+y)\\
=(x+y)-\dfrac{2u(x-y)^{\top}(x+y)}{\|u\|^2}\\
=(x+y)-\dfrac{2u(\|x\|^2-\|y\|^2)}{\|u\|^2}$
ここで、$\|x\|=\|y\|$ であることを使うと、第二項が $0$ になることが分かり、$P(x+y)=x+y$ となります。
固有値 -1 を持つこと
鏡映変換においては、折返しライン(垂直二等分線)に垂直なベクトルは逆向きに変換されるので、$x-y$ が固有値 $-1$ の固有ベクトルであることが分かります。
一応計算でも確認してみます:
$P(x-y)\\
=(x-y)-\dfrac{2uu^{\top}}{\|u\|^2}u\\
=(x-y)-2u\\
=-(x-y)$
ハウスホルダー変換の応用
$x,y$ をうまく選んで、ハウスホルダー変換を繰り返すことで、
・任意の対称行列を、三重対角行列に変形できます。
・任意の正方行列を、上ヘッセンベルグ行列(Hessenberg Matrix)に変形できます。
参考:固有値解析
次回は 行列のpノルムの定義と性質 を解説します。
