このページでは、命題の逆、裏、対偶の意味と具体例をそれぞれ解説します。数学の問題でも重要ですが、日常会話でも「逆、裏、対偶」という言葉を使う人がいるので、知っておいた方が良い知識です。
逆とは
例えば,
「$x\geq 2$ ならば $x^2\geq 4$」
という命題の逆は、
「$x^2\geq 4$ ならば $x\geq 2$」
です。
このように、逆とは、仮定と結論を交換した命題のことです。
ちなみに、上記の例では、もとの命題は真ですが、逆は偽です。なぜなら、例えば $x=-3$ とすると、$x^2\geq 4$ ですが $x\geq 2$ ではありません。
裏とは
例えば,
「$x\geq 2$ ならば $x^2\geq 4$」
という命題の裏は、
「$x <2$ ならば $x^2 < 4$」
です。
このように、裏とは、仮定と結論を否定したような命題のことです。
ちなみに、上記の例では、もとの命題は真ですが、裏は偽です。なぜなら、例えば $x=-3$ とすると、$x <2$ ですが $x^2 < 4$ ではありません。
対偶とは
例えば,
「$x\geq 2$ ならば $x^2\geq 4$」
という命題の対偶は、
「$x^2 < 4$ ならば $x < 2$」
です。
このように、対偶とは、仮定と結論をいれかえてそれぞれを否定したような命題のことです。
ちなみに、上記の例では、もとの命題も対偶も真です。
もとの命題と対偶の真偽は一致する
・上の具体例からなんとなく分かるように、もとの命題が真なら、その対偶も真です。もとの命題が偽なら、その対偶も偽です。
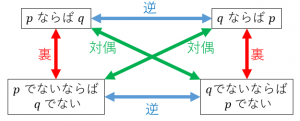
・図において逆は横移動、裏は縦移動、対偶は斜め移動です。つまり、逆の裏は対偶です。また、「対偶の逆は裏」「対偶の裏は逆」なども成り立ちます。
日常会話における具体例
例題
「休日はお客さんが少ない」の逆、裏、対偶を述べよ。また「休日はお客さんが少ない」という主張が正しいとき、逆、裏、対偶がそれぞれ正しいかどうか考えよ。
解答
もとの主張は「休日ならお客さんが少ない」です。$p$「休日」 $q$「お客さんが少ない」です。
逆:
逆は仮定と結論を入れ替えるので「お客さんが少ないなら休日」です。平日もお客さんが少ないかもしれないので、この主張は正しいかどうかは分かりません。
裏:
裏は仮定と結論を否定するので「平日ならお客さんが多い」です。平日もお客さんが少ないかもしれないので、この主張は正しいかどうかは分かりません。
対偶:
対偶は入れ替えてひっくり返すので「お客さんが多いなら平日」です。休日はお客さんが少ないとき、この対偶の主張も正しいことになります。
ちなみに、日常会話では「その命題は真だ」などと言うとかしこまって聞こえるので「その主張は正しい」くらいの言い方の方がよい気がします。
次回は 数学的帰納法の意味と例題2問 を解説します。
