ざっくり言うと、
全部細かく表すのが同時分布
「合計」を表すのが周辺分布
一部を固定したのが条件付き分布
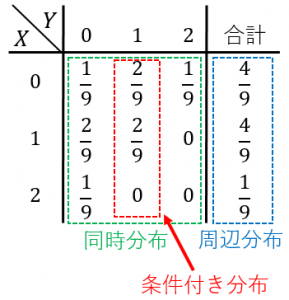
同時分布の例
2つの確率変数 $X$、$Y$ のとる値の全てのペアに対しての確率を表したものが同時分布(結合分布、同時確率分布)です。
例えば、グー、チョキー、パーをランダムで出すジャンケンマシーンを2回動かしたとき、
$X$:グーを出した回数
$Y$:チョキを出した回数
としてみます。
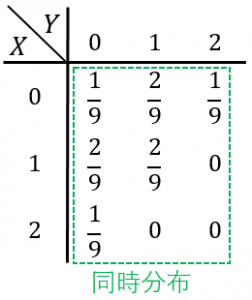
このとき、$X$ と $Y$ の値のペアに対して、それが起こる確率は図のようになります。これを $X$ と $Y$ の関数とみなしたものが同時分布 $P_{X,Y}(x,y)$ です。
例えば、グーが2回連続で出る確率は $\dfrac{1}{9}$ なので、
$P_{X,Y}(2,0)=\dfrac{1}{9}$ です。
周辺分布の例
例えば、ジャンケンマシーンの例で、
$X$:グーを出す回数 には興味があるが、
$Y$:チョキを出す回数
には興味がないときには、図の青い部分だけ分かれば十分です。これが周辺分布です。
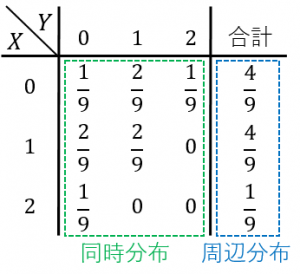
このように、同時分布(情報は多いけど興味のない変数も含まれている)から周辺分布(興味がある変数の情報だけを取り出したもの)を求めることを周辺化と言います。
具体的には、$P_X(x)=\displaystyle\sum_{y=0}^2P_{X,Y}(x,y)$
のように興味がない確率変数について、和を取ることで周辺分布を得ることができます。
$\dfrac{1}{9}+\dfrac{2}{9}+\dfrac{1}{9}=\dfrac{4}{9}$
のような感じです。
条件付き分布の例
例えば、ジャンケンマシーンの例で、
$Y$:チョキを出した回数 が $1$ 回
ということが分かってしまえば、同時分布(表全体)のうち必要なのは図の赤い部分だけです。
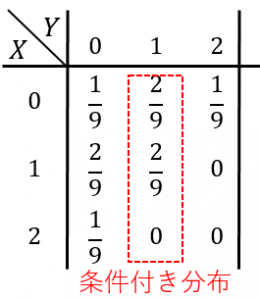
これが条件つき分布 $P_{X\mid Y}(x\mid 1)$ です。
連続分布の場合
・同時確率密度関数:$f_{X,Y}(x,y)$ は2変数関数になります。
$a\leq X\leq b$ かつ $c\leq Y\leq d$ となる確率は、
$\displaystyle\int_a^bdx\int_c^ddyf_{X,Y}(x,y)$
となります。
・周辺分布の密度関数は、同時確率密度関数を「足し上げたもの」つまり、積分になります:
$f_X(x)=\displaystyle\int f_{X,Y}(x,y)dy$
$f_Y(y)=\displaystyle\int f_{X,Y}(x,y)dx$
・条件つき分布の密度関数は、単純に一部の変数に値を代入したものです:
$f_{X\mid Y}(x\mid 2)=f_{X,Y}(x,2)$
のような感じです。
次回は 条件付き独立の意味と例 を解説します。
