AUCとROC曲線について、意味を詳しく解説します。また、AUCの性質を3つ紹介します。
AUCとは
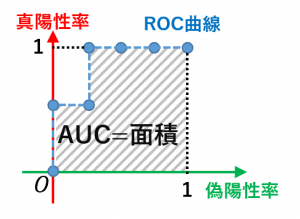
AUCは、Kaggle などのデータ分析コンペでも用いられる有名な指標です。
「2クラス分類」という問題設定や、ROC曲線、真陽性率、偽陽性率の意味については後述します。
AUCを理解するための問題設定
本当の正解は、AとBが陽性でそれ以外が陰性とします。

正解を知らない人が、ある検査方法によって、それぞれが陽性である確率を推定して、上記のようになったとします。
ある程度うまく判別できているように見えますが、この検査方法はどれくらい「良い方法」と言えるでしょうか?この「良さ」を表す評価指標の1つがAUCです。
ROC曲線とは
ROC曲線とは、
「推定確率が $p$ 以上のものを陽性とみなす」とき、縦軸:真陽性率、横軸:偽陽性率、に対応する点を、あらゆる $p$ に対してプロットしてつなげた折れ線グラフです。
ただし、真陽性率とは、本当に陽性のものの中で、正しく陽性とみなせた割合です。
偽陽性率とは、本当に陰性のものの中で、間違って陽性とみなした割合です。
ROC曲線の例
さきほどの具体例で考えてみます。
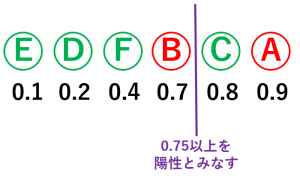
$p=0.75$ とすると、本当に陽性のもの(AとB)の中で正しく陽性とみなせたもの(A)の割合は、$\frac{1}{2}$ です。本当に陰性のもの(C、D、E、F)の中で間違って陽性とみなしたもの(C)の割合は、$\frac{1}{4}$ です。そこで、$(\frac{1}{4},\frac{1}{2})$ をプロットします。
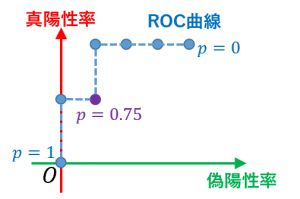
他のあらゆる $p$ についてもプロットして、折れ線でつなげたものがROC曲線です。
ROC曲線の性質
$p$ を小さくすると「陽性とみなす」ものの数が増えます。つまり、真陽性率も偽陽性率も上がります。そのため、$p$ を小さくすると、点は右上(上または右)に進んでいきます。ROC曲線は、$p=1$ に対応する点 $(0,0)$ からスタートして、$p=0$ に対応する点 $(1,1)$ まで進む折れ線です。
その際、良いモデルの場合は真陽性率の方が早く上がるので、上に早く進みます。悪いモデルの場合は偽陽性率の方が早く上がるので、右に早く進みます。
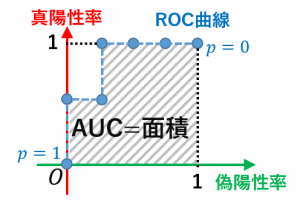
つまり、良いモデルの場合、AUC(右下部分の面積)が大きくなり、悪いモデルの場合、AUCは小さくなります。
AUCの性質
最悪の場合(完全に右に進んでから上に行く)AUCは0です。
最高の場合(完全に上に進んでから右に行く)AUCは1です。
ランダムな分類の場合、しきい値 $p$ をどこに設定しても、真陽性率と偽陽性率は同じくらいになります。つまり、ROC曲線が $y=x$ 付近になるため、AUCは0.5くらいになります。
つまり、順番が変わらない範囲でモデルの出力確率を動かしてもAUCは変わりません。これは、ROC曲線の構成方法から分かる性質です。
次回は クラス分類とクラスタリングの意味と違い を解説します。
