atan、atan2 はいずれもタンジェントの逆関数(アークタンジェント)にまつわる関数ですが、少し違いがあります。
atan関数とは
例えば、$\tan\dfrac{\pi}{3}=\sqrt{3}$ なので、$\mathrm{atan}(\sqrt{3})=\dfrac{\pi}{3}$ になります。
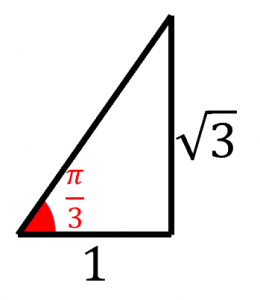
入力の範囲(定義域)は全ての実数、出力の範囲(値域)は $-\dfrac{\pi}{2}$ より大きく $\dfrac{\pi}{2}$ より小さい値です。
atan2関数とは
例えば、$(1,\sqrt{3})$ の偏角は $\dfrac{\pi}{3}$ なので、$\mathrm{aran2}(1,\sqrt{3})=\dfrac{\pi}{3}$ になります。
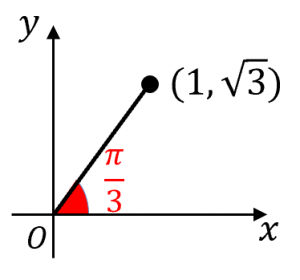
入力の範囲は2つの引数とも全ての実数です。出力の範囲は、$-\pi$ から $\pi$ の間です。
※プログラミング言語によっては、引数 $(x,y)$ の順番が逆になって $\mathrm{atan2}(y,x)$ の形になることもあります。
例えば、EXCEL は $(x,y)$ の順番で、python は $(y,x)$ の順番です。
atanとatan2の関係
$x>0$ のとき、
$\mathrm{atan}\left(\dfrac{y}{x}\right)=\mathrm{atan2}(x,y)$
が成立します。
また、出力の範囲は、
$-\dfrac{\pi}{2}<\mathrm{atan}(x)<\dfrac{\pi}{2}$
$-\pi<\mathrm{atan2}(x,y)<\pi$
のように異なることも注意が必要です。
単純にタンジェントの逆関数の値を計算したいときには $\mathrm{atan}$、直交座標の点の偏角を求めたいときには $\mathrm{atan2}$ を使います。
次回は Rで二項分布の計算をする(dbinomなど) を解説します。
