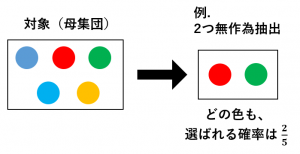
無作為抽出(ランダムサンプリング)とは、対象の中から「ランダムに」つまり、等しい確率で選ぶことを表します。
無作為抽出を行う具体的な方法
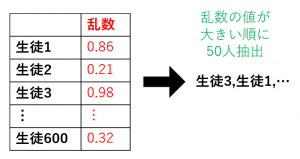
手順1. 生徒 $600$ 人を左の列に並べる
手順2. 乱数を $600$ 個発生させて、2列目に並べる
手順3. 乱数の値が大きい順に $50$ 個抽出する
※手順2は、例えばエクセルではRAND関数を使って行うことができます。2列目(B列)に =RAND() と入力します。
多段抽出法
母集団の大きさが大きすぎる場合(例えば、日本人全員)、上記の手順で無作為抽出を行うことが難しいです。
無作為抽出の目的
ある高校の生徒数は $600$ 人であるとします。この高校の生徒の平均身長を知りたいという状況を考えます。
一番シンプルで正確な方法は、$600$ 人全員の身長を測って平均を取ることです(この方法を全数調査と言います)。
しかし、$600$ 人測るのは大変です。そこで、例えばランダムに $50$ 人選んで、その平均を全体の平均の近似値とみなすという手法が考えられます。
このような場合に、ランダムに(等しい確率で)選ぶという行為(無作為抽出)が必要になります。選ぶ数(この例だと $50$)を標本数と言います。
無作為抽出は難しい
無作為抽出は全数調査より楽というメリットがある反面、一部分だけを調べるので誤差が生じます。
ダメな(無作為抽出でない)例:
・(さっきの例について)$600$ 人の身長を測るのはめんどうなので、1クラスの生徒の身長の平均を取る。
→例えば高校3年のクラスを選ぶと、全体の平均より高くなってしまうことが予想される。
・日本人全員についての意見をまとめたいが、めんどくさいので東京の人にのみアンケートを配る
→意見が偏ってしまう。
・日本人全員についての意見をまとめたいので、全都道府県から無作為に100人ずつ選んでアンケートを配る
→人口の多い都道府県の人は、人口の少ない都道府県の人よりも選ばれにくいので、厳密には完全なランダムサンプリングではない。
次回は 母平均、標本平均、および標本平均の平均 を解説します。
