交差エントロピーとは、
・2つの確率分布がどれくらい「離れているか」を表す指標です。
・分類問題の予測の正しさの指標として使えます。
交差エントロピー(クロスエントロピー)について、具体例を使って紹介します。ニューラルネットワークのパラメータ学習の際に必要になる微分の計算も行います。
交差エントロピーの定義
$-\displaystyle\sum_{x}P(x)\log Q(x)$
を交差エントロピー(クロスエントロピー)と言います。
後ほど具体例で見るように、$P$ と $Q$ が似ている分布のとき、交差エントロピーは小さくなります。
交差エントロピーは、機械学習(2値分類、多値分類)における予測の誤差として使われることが多いです。実際、$P$ を「正解の分布」、$Q$ を「予測の分布」とすると、機械学習による予測が正解に似ているほど、$P$ と $Q$ の交差エントロピーが小さくなると考えることができます。
2値変数の交差エントロピー
例えば、$P$ も $Q$ も二値変数(ベルヌーイ分布)の場合
つまり、
$P(x_1)=p$、$P(x_2)=1-p$
$Q(x_1)=q$、$Q(x_2)=1-q$
のとき、
交差エントロピーは、
$-p\log q-(1-p)\log(1-q)$
となります。
いろいろな $p$ と $q$ に対して交差エントロピーを計算してみました:
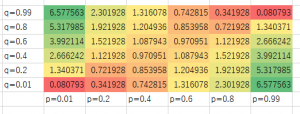
$p$ と $q$ が近いほど、交差エントロピーの値は $0$ に近くなっています。
ニューラルネットワークの誤差関数
特に、活性化関数をシグモイド関数として、誤差関数を交差エントロピーとしたニューラルネットワークでは、学習に必要な勾配の計算式がシンプルになります。
上の事実を理解するために、以下のようなニューラルネットワークを考えてみましょう:
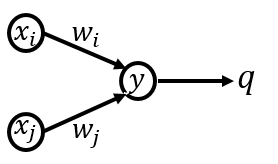
入力:$x$
重み:$w$
途中の値:$y=\sum x_iw_i$
活性化関数:$q(y)=\dfrac{1}{1+e^{-y}}$(シグモイド関数とします)
目標となる出力:$p$
実際の出力:$q=q(y)$
交差エントロピー誤差関数:$E=-p\log q-(1-p)\log (1-q)$
さきほど見たように、$p\fallingdotseq q\fallingdotseq 0$ のときと、$p\fallingdotseq q\fallingdotseq 1$ のときは $E\fallingdotseq 0$ となり、それ以外のときはより大きい値になるので、2クラス分類問題に使えそうですね。
交差エントロピーの微分
ニューラルネットワークの学習を勾配法を使って行う場合には、パラメータによる偏微分が必要になります。そこで、誤差関数のパラメータ $w_i$ による偏微分 $\dfrac{\partial E}{\partial w_i}$ を計算してみます。
合成関数の微分公式を使うと
$\dfrac{\partial E}{\partial w_i}=\dfrac{\partial y}{\partial w_i}\cdot\dfrac{\partial q}{\partial y}\cdot\dfrac{\partial E}{\partial q}$
となります。3つの部分をそれぞれ計算すると、
・ただの一次式の微分:
$\dfrac{\partial y}{\partial w_i}=x_i$
・シグモイド関数の微分:
$\dfrac{\partial q}{\partial y}=(1-q)q$
・交差エントロピーの微分:
$\dfrac{\partial E}{\partial q}=-\dfrac{p}{q}+\dfrac{1-p}{1-q}$
となります。
これらをかけ合わせて整理すると、
$\dfrac{\partial E}{\partial w_i}=x_i\{-p(1-q)+(1-p)q\}
\\=x_i(q-p)$
となり、シンプルな式になりました!
多クラス分類の場合
$P$ も $Q$ も多値変数の場合
つまり、
$P(x_i)=p_i\:(i=1,\dots, n)$
$Q(x_i)=q_i\:(i=1,\dots, n)$
のとき、
交差エントロピーは、
$-\displaystyle\sum_{i=1}^np_i\log q_i$
となります。
次回は ヒンジ関数の意味、損失関数として使えることの大雑把な説明 を解説します。
