行列の積の計算方法と例題

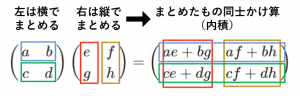
具体例（いろいろなサイズの行列積）

$1\times 2$ 行列と $2\times 1$ 行列の積
$\begin{pmatrix} a &b\end{pmatrix}\begin{pmatrix}c\\d\end{pmatrix}=ac+bd$
→二次元ベクトルの内積

$1\times 3$ 行列と $3\times 1$ 行列の積
$\begin{pmatrix} a &b&c\end{pmatrix}\begin{pmatrix}d\\e\\f\end{pmatrix}=ad+be+cf$
→三次元ベクトルの内積

$2\times 2$ 行列と $2\times 1$ 行列の積
$\begin{pmatrix} a &b\\c&d\end{pmatrix}\begin{pmatrix}e\\f\end{pmatrix}=\begin{pmatrix}ae+bf\\ce+df\end{pmatrix}$

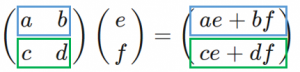
→左側の行列は横に区切る

$1\times 2$ 行列と $2\times 2$ 行列の積
$\begin{pmatrix} a &b\end{pmatrix}\begin{pmatrix}c&d\\e&f\end{pmatrix}=\begin{pmatrix}ac+be&ad+bf\end{pmatrix}$

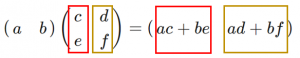
→右側の行列は縦に区切る

$2\times 2$ 行列と $2\times 2$ 行列の積
$\begin{pmatrix} a &b\\c&d\end{pmatrix}\begin{pmatrix}e&f\\g&h\end{pmatrix}$$=\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}$

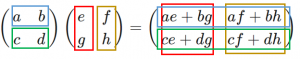
→左は横、右は縦に区切る

全てを覚える必要はありません、左は横、右は縦に区切ると覚えましょう。

かけ算が定義できないサイズもある

例えば、$1\times 2$ 行列と $1\times 2$ 行列のかけ算、などは定義できません。

３×３行列の例題

問題

$A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}$、
$B=\begin{pmatrix}10&11&12\\13&14&15\\16&17&18\end{pmatrix}$
とする。行列のかけ算 $AB$ の$21$ 成分を求めよ。また、$BA$ の $21$ 成分も求めよ。

答え

$AB$ の $21$ 成分は、$A$ を横に区切った二つ目：$\begin{pmatrix}4&5&6\end{pmatrix}$
と $B$ を縦に区切った一つ目：$\begin{pmatrix}10\\13\\16\end{pmatrix}$ の内積なので、
$4\cdot 10+5\cdot 13+6\cdot 16\\
=40+65+96=201$

同様に、$BA$ の $21$ 成分は、$B$ を横に区切った二つ目：$\begin{pmatrix}13&14&15\end{pmatrix}$
と $A$ を縦に区切った一つ目：$\begin{pmatrix}1\\4\\7\end{pmatrix}$ の内積なので、
$13\cdot 1+14\cdot 4+15\cdot 7\\
=13+56+105=174$

このように、$AB$ と $BA$ は一般には異なります（行列の積は順番を交換したら結果が変わる）。

次回は ベクトルと行列の積の基本的な５つの式 を解説します。