動径基底関数(RBF)に関連する用語・知識を整理しました。
動径関数とは
例えば、
・$f_\overrightarrow{c}(\overrightarrow{x})=\|\overrightarrow{x}-\overrightarrow{c}\|^2$
・$f_\overrightarrow{c}(\overrightarrow{x})=\exp(-\gamma\|\overrightarrow{x}-\overrightarrow{c}\|^2)$
などは動径関数です。
(このページでは、添字の $\overrightarrow{c}$ は動径関数の中心を表します)
動径基底関数(RBF)
動径関数は「基底のように」使われることがしばしばあり、そのような文脈では動径基底関数(Radial Basis Function, RBF)と呼ばれることがあります。
「基底のように」とは、
・($\overrightarrow{c}$ をいろいろ変化させた)同じ種類の動径関数を集めてきて
・それらの線形和を取ることでいろいろな関数を近似する
というイメージです。
RBFカーネル
動径関数の例として、
$f_\overrightarrow{c}(\overrightarrow{x})=\exp(-\gamma\|\overrightarrow{x}-\overrightarrow{c}\|^2)$
を考えてみます。$\gamma$ は正の定数です。
($\overrightarrow{x}$ の関数とみなすこともできますし、$\overrightarrow{x}$ と $\overrightarrow{c}$ の関数とみなすこともできます)
$\overrightarrow{x}$ が $\overrightarrow{c}$ から遠くなると、この関数の値は急激に $0$ に近づいていきます。
この関数はSVMなどにおけるカーネル関数として使われることがあり、その文脈ではRBFカーネル(ガウスカーネル、ガウシアンカーネル)と呼ばれることがあります。
関連:ガウスカーネルとその特徴ベクトル
RBFネットワーク
・(中心 $\overrightarrow{c}$ をいろいろ変化させた)同じ種類の動径関数 $f_{\overrightarrow{c_i}}(\overrightarrow{x})$ を集めてきて
・それらの線形和を取った
$\displaystyle\sum_{i=1}^nw_if_{\overrightarrow{c_i}}(\overrightarrow{x})$
のような関数を考えます。
関数の入力は、$\overrightarrow{x}=(x_1,\dots,x_m)\in\mathbb{R}^m$ で、出力は実数です。これは、$\overrightarrow{c_1},\dots,\overrightarrow{c_n}$ と $w_1,\dots,w_n$ を適切に動かす(学習させる)ことで、いろいろな関数を表すことができます。
そして、このような関数は図のようなネットワークを使って表現できるため、RBFネットワークと呼ばれることがあります。
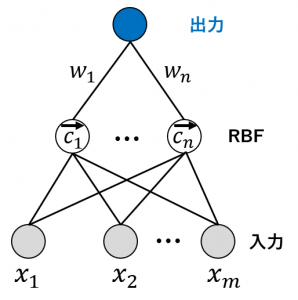
RBFネットワークと聞くと難しそうですが、要するに緑色の式のような関数のことです。
RBF補間
緑色の式の関数は、関数の補間に使えます。補間とは、与えられた $(\overrightarrow{x_1},y_1),\dots,(\overrightarrow{x_n},y_n)$ という $n$ 個の点を通る関数を求める(ことによって、与えられていない $\overrightarrow{x}$ における値も予測する)問題です。
例えば、
・与えられた点から中心を $\overrightarrow{c_i}=\overrightarrow{x_i}$ で定め
・$y_i=\displaystyle\sum_{i=1}^nw_if_{x_i}(\overrightarrow{x_i})$ となるような $w_1,\dots,w_n$ を定める。
という方法で $n$ 点を通る関数 $\displaystyle\sum_{i=1}^nw_if_{\overrightarrow{c_i}}(\overrightarrow{x})$ を構成できます。このようなRBFを用いた補間をRBF補間と言います。
次回は 双線形性、多重線形性の意味と例 を解説します。
