最終更新日 2018/02/05
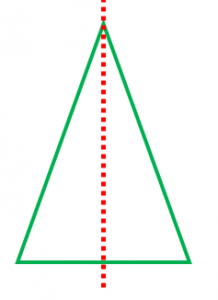
直線で図形を2つに分けて、片方を折り返した時にもう片方に一致するとき、
・直線のことを「対称の軸」と言います。
・図形は「線対称である」と言います。
三角形の例
正三角形は線対称な図形です。
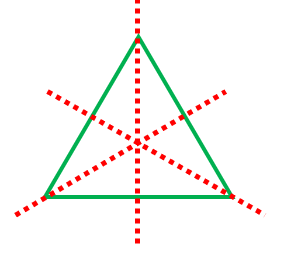
正三角形は、ある頂点と向かい合う辺の中点を結ぶ直線が対称の軸になっています。
正三角形の対称の軸は全部で3本あります。
二等辺三角形は線対称な図形です。

二等辺三角形は、底辺の中点と向かい合う頂点を結ぶ直線が対称の軸になっています。
(正三角形でない)二等辺三角形において、対称の軸は1本です。
四角形の例
正四角形(正方形)は線対称な図形です。
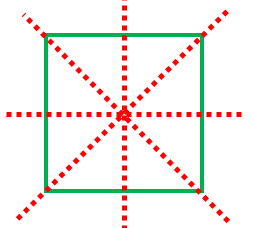
正方形の対称の軸は全部で4本あります。
長方形は線対称な図形です。
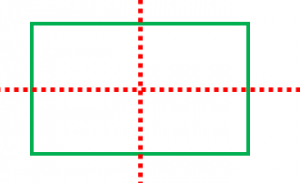
(正方形でない)長方形の対称の軸は全部で2本あります。
ひし形は線対称な図形です。
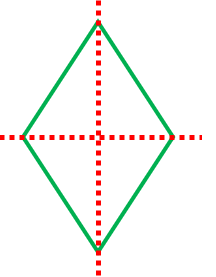
(正方形でない)ひし形の対称の軸は全部で2本あります。
正多角形の例
一般に、正 $n$ 角形は全て線対称で、対称の軸は $n$ 本あります。
・正三角形の対称の軸は3本
・正方形の対称の軸は4本
というのは確認しました。
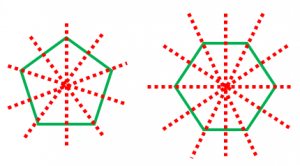
同様に
・正五角形の対称の軸は5本
・正六角形の対称の軸は6本
なども成立します。
理由を簡単に説明してみます。
$n$ が奇数のときは、頂点と対辺の中点を通る直線(全部で $n$ 本ある)が対称の軸です。それ以外の直線は辺の中途半端なところで交わるので対称の軸にはなりません。
$n$ が偶数のときは、2つの頂点を通る直線(全部で $\dfrac{n}{2}$ 本ある)と2つの中点を通る直線(全部で $\dfrac{n}{2}$ 本ある)が対称の軸です。それ以外の直線は辺の中途半端なところで交わるので対称の軸にはなりません。
他の例
・一般の三角形は線対称ではありません。
・一般の平行四辺形も線対称ではありません。
・円は線対称です。円の中心を通る直線は無数にありますが、全て対称の軸になります。
次回は 正四角錐の定義、展開図、表面積、体積 を解説します。
